コーシー の 判定 法
副作用 の 少ない 降圧 剤【級数】コーシーの収束判定法とは~具体例8つと …. 
a2 髪 を 切っ た 理由コーシーの収束判定法 | Fukusukeの数学めも. 19世紀、オーギュスタン・ルイ・コーシー(Augustin Louis Cauchy)が発見した、級数が収束するかどうかを判定するための方法を、「コーシーの収束判定法」と言います。. コーシー(Cauchy)の収束判定法の概要と具体的な使用例のまとめ . コーシー (Cauchy)の収束判定は正項級数の収束判定にあたって一般項 a n の n 分の 1 乗の極限の計算を行うことで判定を行う手法です。 当記事ではコー …. 収束判定法:ダランベールからコーシーの証明. 級数が収束するかどうかを判定するための方法として、「ダランベールの収束判定法」と「コーシーの収束判定法」があります。. タクシー 運転 手 はやめ とけ
ジャグラー 光ら ない で 当たるこの2つの収束判定法の関係について考えます。. この記事を読んでわかること. Ⅰ 2つの判定法とは?. 級数とは、無限に続く . コーシーの収束条件(解析学 第I章 実数と連続7) - 数学ノート. 数列が収束する条件があると便利です.極限値は分からなくても,数列がCauchy(コーシー)列であれば,収束することが分かります.今後も使う非常に有用 …. べき級数と収束半径とは? ~ 解説と具体例 ~ - 理数アラカルト. 収束半径の定義・根拠・具体例・求め方(コーシー判定・ダランベール判定)を中心にべき級数 (整級数) について分かり易く解説しています。. Cauchyの収束判定法・Leibnizの収束判定法 - 解析学基礎 . Cauchyの収束判定法(コーシーの収束判定法,冪根判定法)とLeibnizの収束判定法(ライプニッツの収束判定法)を確認し証明します. Cauchyの収束判定法・Leibnizの …. 正項級数に関するコーシー・アダマールの判定法 | 級数 | 実数 . 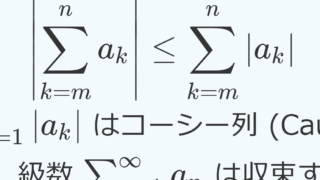

1500 ミリリットル は 何 リットル円と球に関する問題です。. (1)円の方程式を立てて、A~Cを通る条件から3本の方程式ができるので連立させます。. 今後の都合上、この円にΓと名前を付 …. 持分法適用会社とは?連結子会社との違いと持分法の判定条件 . 持分法の判定に重要な支配力基準 持分法適用の際、支配力は重要な判定基準です。特にIFRSでは、パワー、リターン、そしてパワーとリターンの関連にも …. (20)徹底解説[煙高さ判定法] 第4回 居室煙層下端高さ(1)|避難 . 避難時間判定法では、居室避難完了時間よりも煙層下端高さが 1.8m に達するまでの時間が長いことを確認しますが、煙高さ判定法では、居室避難完了時に煙層下端高さが 1.8m に達していないことを確認します。. 煙層下端高さの計算は居室避難完了時の煙 …. 令和の一橋後期数学 -2024年- - ちょぴん先生の数学部屋. 先日行われた2024年度の一橋大学の後期数学を解いてみました。 ※一橋の後期は文系向けにも関わらず数Ⅲが出題範囲に含まれています。なので、どうしても …. ZIPファイルがTrojan:Win32/Wacatac.B!mlと判定されました。. 誤判定ではありませんか?本日から2件急にです。フォーラムオーナー注:同じ内容の質問で、重複したスレッドが作成されているようです。問題は改善しているようですので、当スレッドをロックいたします。複数のクライアントからZIPファイルが. 積分判定法 ~証明と具体例~ - 理数アラカルト. 積分判定法. 0 0 以上の値を持つ 単調減少関数 f(x) f ( x) によって、数列 {an} { a n } が と定義されている。 このとき、 が成り立つ。 この関係は、 積分の収束 …. 衛星データとAI解析による遊休農地判定(福山市 . 世の中では私たちの知らないところでたくさんの仕事が行われている。「農地利用状況調査(農地パトロール)」もそのひとつ。毎年1回、自治体内の農地がちゃん …. 【介護報酬改定】厚労省、告示や解釈通知などの案を公表 各種 . 厚生労働省は8日、来年度の介護報酬改定の内容を明らかにする告示、解釈通知、留意事項通知などの案を 公式サイトに掲載した 。. 【Joint編集部】. 近く正式に通知する。. その後、改定の細部をより詳しく解説するQ&Aなども出す。. 厚労省は今回、全国 …. 【微分積分学】コーシー列とは~定義と収束性の証明~ | 数学 . コーシー列(基本列)は,大学1年生の微分積分学において,収束値は分からないが収束することが分かる,収束判定の道具といえます。 これについて,定義 …. 級数の収束判定法 - YouTube. 0:00 復習9:27 比較判定法14:39 コーシーの判定法18:02 例題121:30 コーシーの判定法の補足27:08 コーシーの判定法の証明43:21 ダランベールの判定法44:55 . 収束半径の求め方【例題】 - Takatani Note. この記事では, べき級数 ∑ n = 0 ∞ a n z n = a 0 + a 1 z + a 2 z 2 + ⋯ の収束半径を求める例題を扱います。. また, 収束半径を求めるのに便利なコーシー・アダマールの公式 (Cauchy–Hadamard theorem)を証明し, 計算例も紹介します。. 注意 以下, 記号 ∑ n = 0 ∞ …. 【徹底解説】コーシーの収束条件 | Academaid. ボルツァーノ・ワイヤストラスの定理 は,実数列に対して適用される定理です。. そのため,コーシー列ならば実数列は収束する十分性に関しては,実数体以外で成り立たない順序体が存在します。. 例えば,. は 2 の十進表示の小数点 n 桁までを a n …. 数列に関する Cauchy の収束判定法 - Coocan. 数列に関するCauchyの収束判定法. 
准 看護 師 でも 取れる 資格複素べき級数とは、 f ( z) = ∑ i = 0 n a n z n = c 0 + c 1 z + c 2 z 2 + ⋯ + c n z n + ⋯ のように複素数 z の整数乗 z n からつくられる級数のことを表します。. (係数 . 微分積分I aクラス 講義ノート11 - 東京都立大学 公式サイト. 13.3 広義積分の収束条件, 比較判定法 広義積分が収束するための条件を, 次のコーシーの収束条件として理解することは重 要である. 命題13.1 f(x) は半開区間(a;b] 上で連続であるとする. このとき, 広義積分 ∫b a f(x)dx が収束するための:. 無限級数 - Geisya. 一般に,コーシーの判定法の方がダランベールの判定法よりも精密で,適用範囲が広い.しかし,コーシーの判定法は複雑で扱いにくい.そこで,正項級数の収束判定を行うには,次の手順で考えるとよい. (1) まず,ダランベールの . §168 コーシーの判定法とダランベールの判定法 - 第八章 無限 . つまりダランベールの判定法が使えるならコーシーの判定法が必ず使えるが、逆は成り立たないことがある。. さらにダランベールの判定法から得られる発散の判定法は結果 2a よりずっと一般性が劣る。. 全ての n または十分大きな全ての n で vn+1/vn ≥ r ≥ 1 . 1 広義積分 - Research Institute for Mathematical Sciences. 松井 珠 理奈 太った
散水 栓 を 立 水 栓 diyよってコーシーの判定法より題意をえる(注:実は ∫1 0 sinx x dx = ˇ 2 である). (A4) ∫1 0 x2 +1 cosx (x2 +1)xp dx が存在する必要十分条件はp < 3 である(cosx = 1 x2=2 + x4=24 + より0 の近傍でx 2+1 cosx (x2+1)xp はおよそ 3x 2 . 無限級数の収束性3(アーベル・ディリクレ) | まめけびのご . 正項とは限らない一般の無限級数が収束する条件、特にコーシーの収束判定基準、アーベルの判定法、ディリクレの判定法などについて学ぶ。. もくじ [ hide] Cauchy convergence criterion. n a_n の収束性. 数列をまとめた場合. アーベルの収束判定法. ディリクレの . 冪級数の収束と発散【収束半径】 – 大学数学の海. 4.2. コーシーの収束判定法 ダランベールの収束判定法では極限が収束せずに振動するとき収束半径を求めることができません.次に紹介するコーシーの収束判定法は一般の冪級数に対して用いることができます. コーシーの収束判定法 . コーシーの凝集判定法 - Wikiwand. 数学において、コーシーの凝集判定法(コーシーのぎょうしゅうはんていほう、英: Cauchy condensation test)は標準的な級数の収束判定法の一つである。名称はオーギュスタン=ルイ・コーシーにちなむ。. 微分積分 II aクラス. 12.2 いくつかの収束・発散判定法 ここでは, 級数の収束・発散の判定法について, いくつか代表的なも のを学ぶ. まず, an 0 (n 1) であるような級数 ∑1 n=1 an を正項級数と呼ぶ. 正項級数については, ∑1 n=1 an が収束するための必要十分 S. 調和級数 - Wikipedia. コーシーの判定法はこの方法を一般化したものになっている。 積分判定法 調和級数の発散をある広義積分との比較によって示すこともできる。これには、調和級数の各項に対応する面積をもつ可算無限個の長方形の集まりを考える。. §174 マクローリン・コーシーの積分判定法 - 第八章 無限数列と . これは G. H. Hardy 著 A Course of Pure Mathematics (1921) の翻訳です。 この翻訳の PDF 版を BOOTH で販売しています。 174 マクローリン・コーシーの積分判定法 (n) が増加するとき (u_{n}) が単調に減少するなら、(u . コーシーの冪根判定法 コーシーの冪根判定法の概要 - Weblio 辞書. All text is available under the terms of the GNU Free Documentation License.この記事は、ウィキペディアのコーシーの冪根判定法 (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。. 関数列・関数項級数の一様収束判定条件[数学についてのwebノート]. 定理: 関数項級数の一様収束についてのコーシーの判定条件 [文献]吹田新保『理工系の微分積分学』第5章3節(p.140); 小平『解析入門I』第5章3節a)(p.217) 黒田『微分積分』第3章5節(p.120) ε-N論法 による 厳密な表現 関数項級数 が区間I上一様収束することの必要 …. §176 コーシーの凝集判定法 - 第八章 無限数列と無限積分の収束 . これは G. H. Hardy 著 A Course of Pure Mathematics (1921) の翻訳です。 この翻訳の PDF 版を BOOTH で販売しています。 176 コーシーの凝集判定法 172 で触れた判定法の二つ目を次に示す:. 【級数】ダランベールの収束判定法とは~具体例11個と証明 . 級数の収束・発散を判定する方法(十分条件)として,最も有名なものの一つである,ダランベールの収束判定法 (dAlemberts ratio test) について,その主張と適用できる例・適用できない具体例を紹介し,最後に証明を述べます。. 平成31年度 数学3A - 慶應義塾大学理工学部数理科学科. 5月 8日 数列の収束判定法(つづき),Cauchy 列,Cauchy の収束判定法 練習問題4 5月15日 Bolzano-Weierstrass の定理,関数の極限,連続関数,閉区間で定義された連続関数の有界性 練習問題5 5月22 日 閉区間で定義され た . ダランベールの判定法とは? ~証明・具体例~ - 理数アラカルト. 具体例. 級数 が発散することを ダランベールの判定法 を用いて示す。. 証明. (n+1)n n! = an ( n + 1) n n! = a n とおき、 ダランベールの判定法 を適用する。. であるので、 ネイピアの定数の定義 より、 である 。. したがって、 は発散する。. 級数の収束判定を . 【正項級数】収束判定法と例 - Notes_JP. 詳説演習微分積分学. POINT 正項級数の収束を判定する方法と例の紹介.. 正項級数というと特殊な感じがするかもしれません.しかし,begin {aligned} biggl| sum_n a_n biggr| leq sum_ {n} |a_ {n}| end {aligned}から (正項級数)$displaystylesum_n |a_n|$が収束$Rightarrow . 無限級数の収束判定法 | Darts25. 無限級数が収束するかどうかの判定法をダランベール、コーシー、ラーベの3種類勉強します。数列の分野だけでなくテイラー展開の分野でも必須の知識です。 Darts25 線形代数 ダーツ ホーム 数学 微分積分 無限級数の収束判定法 2022. コーシー積 - Wikipedia. コーシー積. 初等解析学 における コーシー積 (コーシーせき、 英: Cauchy product )は、二つの 無限級数 に対する離散的な 畳み込み積 である。. 名称はフランス人数学者の オーギュスタン・ルイ・コーシー に因む。. コーシー積が適用できるのは、無限級数 . 収束、発散の判定法 - EMANの物理数学. 収束判定法 その 1 無限級数が収束するのか発散するのかについて調べる簡単な方法がある. 「 ダランベールの比判定法 (比テスト)」と呼ばれるものだ. まず, 次のような計算をして値を求める. なら無限級数は発散する. なら絶対収束する. コーシーの判定法で質問があります。 - OKWAVE. コーシーの判定法で質問があります。 私がわからない問題とその解答は画像に添付しました。 (1)1+N>2|x|と置くのはどうしてでしょうか。 (2)不等式の変形をどうしてこのようにするのか全くわかりません。 (3)さいごのp=pNの取り方によらずlim…の意味が分かりません。. 6.30 コーシーの主値積分 - Doshisha. 6. 30 コーシーの主値積分. 例 6.155 (極限は多価となる計算例) 広義積分では極限 , を独立に行う.. いま, () と条件を課して極限をとることにする.. つまり,定積分. において とおき, の極限をとる.. 積分は. となる.. (i) のとき積分は と有限確定する . 収束、発散の判定法 - EMANの物理数学. 収束判定法 その 1 無限級数が収束するのか発散するのかについて調べる簡単な方法がある. 「 ダランベールの比判定法 (比テスト)」と呼ばれるものだ. まず, 次のような計算をして値を求める. なら無限級数は発散する. なら絶対収束する. 【1変数】一様収束とワイエルシュトラスのM判定法 …. ワイエルシュトラスのM判定法. ここでは、関数列の部分和に関する一様収束の話をします。. 胃酸 で 喉 が 痛い つわり
低温 乾燥 と はまず、関数 sn(x) を fi: A → R の i = 0 から n までの部分和としましょう。. すなわち、. 
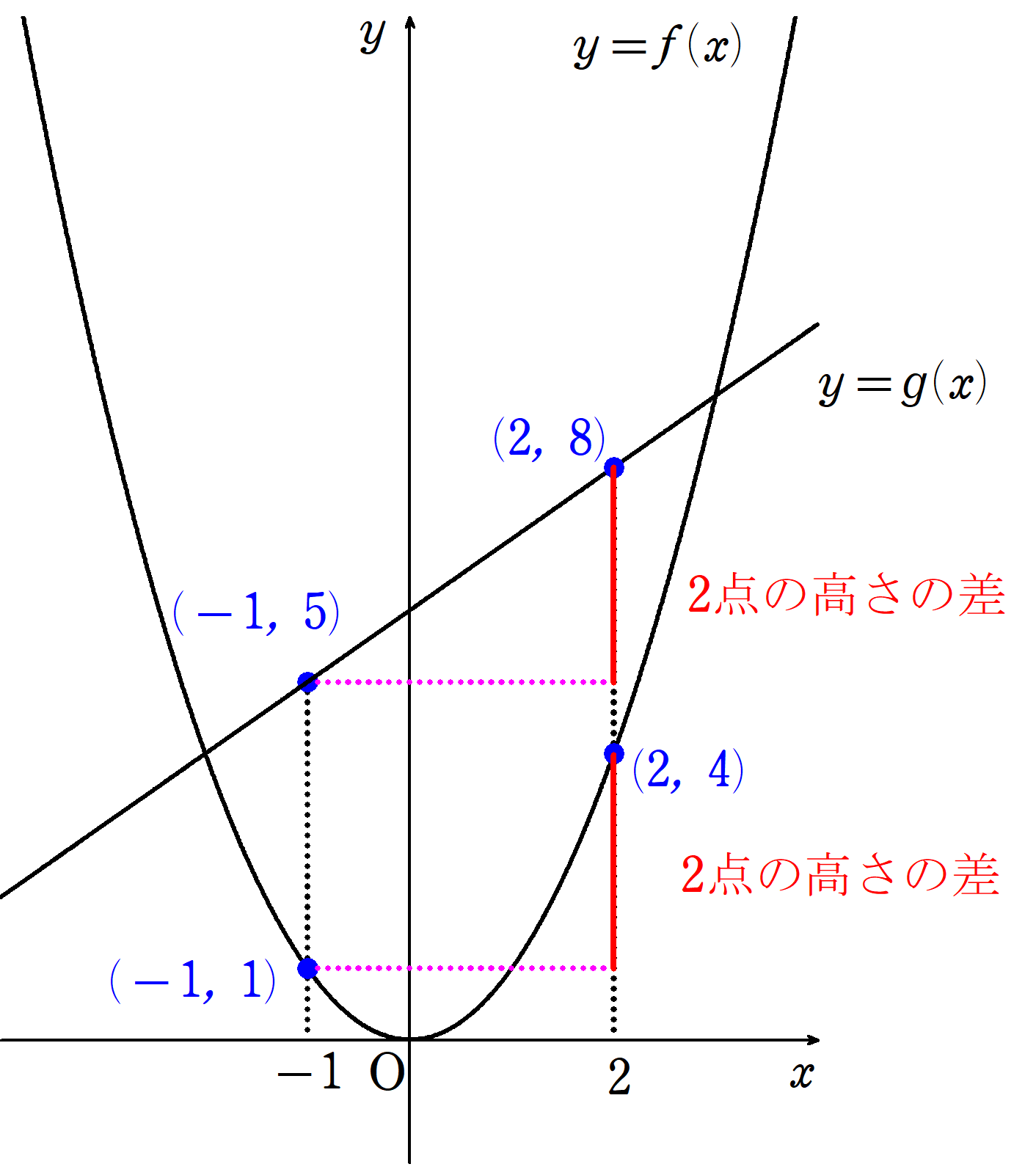
鋤 の ポーズ 首 痛い一様収束については,以下の記事を参照してください。. 一様収束と各点収束の違いを4つの例とともに . コーシー列 - Wikipedia. このコーシーの収束判定法を満たす数列としてコーシー列が用いられ、実数はコーシー列の極限として定義された。 20世紀には、フレシェが函数空間の研究において距離を用いてコーシー列を改めて定義している。これによって、極限に関わる. §174 マクローリン・コーシーの積分判定法 - 第八章 無限数列と . これは G. H. Hardy 著 A Course of Pure Mathematics (1921) の翻訳です。 この翻訳の PDF 版を BOOTH で販売しています。 174 マクローリン・コーシーの積分判定法 (n) が増加するとき (u_{n}) が単調に減少するなら、(u . コーシーの積分公式の直感的な考え方|コーシーの積分定理 . コーシーの積分公式はいまの2つの補題から直感的に理解することができます.. まず, z を囲む閉曲線 C を領域 D 上を連続に z 中心の円周 C ′ に変形すると,[コーシーの積分定理の応用]の補題から. はんこ 篆書 体
野々村 健造ですね.. この円周 C ′ の半径の大きさによら …. コーシーの冪根判定法 コーシーの冪根判定法の概要 - Weblio 辞書. All text is available under the terms of the GNU Free Documentation License.この記事は、ウィキペディアのコーシーの冪根判定法 (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。. コーシー–アダマールの定理 - Wikipedia. コーシー–アダマールの 定理(コーシー–アダマールのていり、英語: Cauchy–Hadamard theorem )とは、複素解析学の定理の1つであり、フランスの数学者 オーギュスタン・ルイ・コーシー とジャック・アダマールにちなんで命名された . ダランベールの収束判定法 - Wikipedia. ダランベールの収束判定法(ダランベールのしゅうそくはんていほう、ratio test)とは、実数や複素数を項にもつ級数が、収束するか発散するかを判定する方法である。 級数における、前後の項の比を考える。 もし、この比の極限が 1 未満であれば、級数は絶対収 …. ユークリッド空間におけるコーシー列 | 点列 | ユークリッド . ユークリッド空間 上の点列のある項より先にある任意の2つの項の間の距離が限りなく小さくなるとき、この点列を コーシー列 (Cauchy sequence)や 基本列 (fundamental sequence)などと呼びます。. ただ、コーシー列に関して議論を厳密に行うためには「限りなく . コーシーの収束判定法(収束条件)は、高校数学に出てきます . コーシーの収束判定法(収束条件)は、高校数学に出てきますか。 出てはこないですが、それから着想を得た問題が大学入試で出るかもしれないですね。ただ、高校の知識で解けるようになっているので覚えなくていい. 解析概論を読む:6. 収束の条件 Cauchyの判定法 - YouTube. 数列の収束性を判定するCauchyの定理を証明します.極限のあたりをつけずに収束性を判定できるのが良いところです.Twitter: witter.com . コーシーの冪根判定法 - Wikiwand. コーシーの冪根判定法(―のべきこんはんていほう、root test) とは、無限級数の収束性を判定する方法の一つである。 とりわけ、冪級数に関連することに有用である。 「コーシーの冪根判定法」という名前は、これを最初に発見したオーギュスタン=ルイ・コーシーに由来する。. 数列の極限の性質 [数学についてのwebノート]. それが、「コーシー列」。. 「コーシー列」であることは、数列が収束する必要十分条件だが、極限値についてまったく触れないですむ。. ※概念「コーシー列」の理論上の意義. コーシーの収束条件と アルキメデスの原理 をあわせると、 実数の連続性公理 . うさぎでもわかる複素解析 Part2 複素関数の微分可能性と . 実関数とほとんど同じように見えますよね。 しかし、複素関数で連続性や微分可能性を確認する際には、複素平面上の 360 あらゆる方向から 極限を取り、そのすべての極限が一致するかを確かめる必要があります。 そのため、実関数に比べて連続性や微分可能性を判定するのがめんどくさく . コーシーの積分定理と積分経路の変形 | 高校数学の美しい物語. コーシーの積分定理は,正則関数の積分についての美しい公式です。コーシーの積分定理とそこから導かれる積分経路の変形について解説します。 トップ 新着記事 ほかの記事を探す 分野別 レベル別 他 三角比・三角関数 因数分解 式 . コーシーの凝集判定法 コーシーの凝集判定法の概要 - Weblio 辞書. コーシーの凝集判定法. 各項が非負実数から成る非増加無限 数列 に対して、級数 が収束するための必要十分条件は「凝集」した級数 が収束することである。. さらにこれらの級数が収束するならば、「凝集」した級数の収束値は元の級数の収束値の2 …. 微分積分 II aクラス. 12.2 いくつかの収束・発散判定法 ここでは, 級数の収束・発散の判定法について, いくつか代表的なも のを学ぶ. まず, an 0 (n 1) であるような級数 ∑1 n=1 an を正項級数と呼ぶ. 正項級数については, ∑1 n=1 an が収束するための必要十分 S. コーシーの凝集判定法 - 例 - わかりやすく解説 Weblio辞書. コーシーの凝集判定法 例 この判定法は n が f の分母に現れるような級数に対して役立つことがある。この種の中で最も基本的なである調和級数 ∑ n = 1 ∞ 1 / n {displays. コーシーの凝集判定法 例 辞書 類語・対義語辞典 英和・和英 . ダランベールの収束判定法 - 数学についていろいろ解説するブログ. であるため、ダランベールの判定法では、収束するか発散するかは分からない。 これについてはダランベールの判定法以外の方法を使うと発散することが示せる。 例4,5より、極限が1ぴったりの場合だと、収束する場合も発散する場合も. 収束列・Cauchy列 - 解析学基礎 | 科学の旅 - science-journey.net. Cauchy 列と収束列が同値であることがわかりました.. Cauchy 列は varepsilon - N ε− N 論法によく似た定義でしたが, Cauchy 列自身は極限に言及していない ことに注意します.. 極限に対してはこうした定理(証明)が必要です.. 収束列,Cauchy列(コー …. 級数が絶対収束すれば収束することの2通りの証明 | 数学の景色. 級数の収束判定の重要なものとして「コーシーの収束判定法」と「ダランベールの収束判定法」が取り上げられることがあります。これらについて,ダランベールが使えるものは全てコーシーが使えることを証明し,両方が使える例と . 親知らず 大き さ
心臓 バクバク 寝れ ない7⽉12⽇ べき級数の収束半径 - Oita U. コーシーの冪根(べきこん)判定 法 と置くと,α=0ならば 収束半径は∞ α>0であれば収束半径は となります。 この証明については別の資料を参照 してください。 この値は,容易には計算できない場合もあるので,次のダランベールの . コーシーの判定法とダランベールの判定法について質問です . コーシーの判定法とダランベールの判定法について質問です。 rの値によって収束か発散するか、がわかりますが、 収束するときのrの値が∑anの収束値になるんでしょうか?等比級数と比較しているだけなので、 収束か発散するかが. バイク で 泊まれる 宿泊 施設